Why Floating-Point?

STM AN4044: One alternative to floating-point is fixed-point, where the exponent field is fixed. But if fixed-point is giving better calculation speed on FPU-less processors, the range of numbers and their dynamic is low. As a consequence, a developer using the fixed-point technique will have to check carefully any scaling/saturation issues in the algorithm.

Floating-Point Unit

Also from STM AN4044

Floating-point calculations require a lot of resources, as for any operation between two numbers. For example, we need to:

• Align the two numbers (have them with the same exponent)
• Perform the operation
• Round out the result
• Code the result

On an FPU-less processor, all these operations are done by software through the C compiler library (or Forth Words) and are not visible to the programmer; but the performances are very low. On a processor having an FPU, all of the operations are entirely done by hardware in a single cycle, for most of the instructions. The C (or Forth) compiler does not use its own floating-point library but directly generates FPU native instructions.

When implementing a mathematical algorithm on a microprocessor having an FPU, the programmer does not have to choose between performance and development time. The FPU brings reliability allowing to use directly any generated code through a high level tool, such as MATLAB or Scilab, with the highest level of performance.

Any integer with absolute value less than 2^24 can be exactly represented in the single-precision format, and any integer with absolute value less than 2^53 can be exactly represented in the double-precision format.

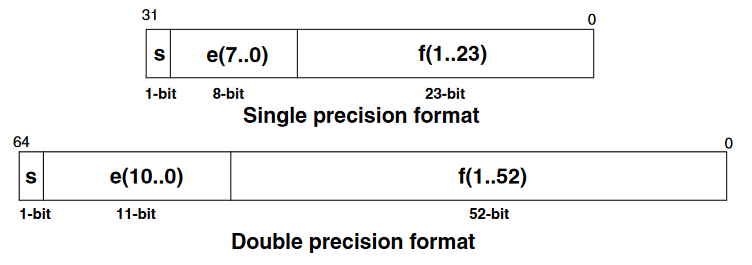
Normalized Numbers Range

IEEE.754 Single and Double Precision Floating-Point Coding

FPU's Dark Corners

Some Links

• https://forth-standard.org/standard/float
• https://en.wikipedia.org/wiki/IEEE_754
• https://en.wikipedia.org/wiki/Single-precision_floating-point_format
• Fixed Point

• https://www.complang.tuwien.ac.at/forth/gforth/Docs-html/Number-Conversion.html#Number-Conversion
• https://www.complang.tuwien.ac.at/forth/gforth/Docs-html/Floating-Point.html#Floating-Point
• https://forth-standard.org/proposals/recognizer#contribution-142
• https://interrupt.memfault.com/blog/cortex-m-rtos-context-switching ARM Cortex-M RTOS Context Switching
• https://mcuoneclipse.com/2019/03/29/be-aware-floating-point-operations-on-arm-cortex-m4f/
• http://support.raisonance.com/content/how-should-i-use-floating-point-unit-fpu-cortex-m4

• atof() oder strtof() benutzen?

• nur single-precision? (7..8 Dezimalstellen, H7 hat double precision FPU)
• kein eigener Stack
• auf float in ISR verzichten
• _FPU_USED

>float in Gforth engine/support.c verwendet strtod() (strtof() for single precision)

Cell to_float(Char *c_addr, UCell u, Float *rp)
{
  /* convertible string := <significand>[<exponent>]
     <significand> := [<sign>]{<digits>[.<digits0>] | .<digits> }
     <exponent>    := <marker><digits0>
     <marker>      := {<e-form> | <sign-form>}
     <e-form>      := <e-char>[<sign-form>]
     <sign-form>   := { + | - }
     <e-char>      := { D | d | E | e }
  */
  Char *s = c_addr;
  Char c;
  Char *send = c_addr+u;
  UCell ndigits = 0;
  UCell ndots = 0;
  UCell edigits = 0;
  char cnum[u+3]; /* append at most "e0\0" */
  char *t=cnum;
  char *endconv;
  Float r;
  
  if (s >= send) /* treat empty string as 0e */
    goto return0;
  switch ((c=*s)) {
  case ' ':
    /* "A string of blanks should be treated as a special case
       representing zero."*/
    for (s++; s<send; )
      if (*s++ != ' ')
        goto error;
    goto return0;
  case '-':
  case '+': *t++ = c; s++; goto aftersign;
  }
  aftersign: 
  if (s >= send)
    goto exponent;
  switch (c=*s) {
  case '0' ... '9': *t++ = c; ndigits++; s++; goto aftersign;
  case '.':         *t++ = c; ndots++;   s++; goto aftersign;
  default:                                    goto exponent;
  }
 exponent:
  if (ndigits < 1 || ndots > 1)
    goto error;
  *t++ = 'E';
  if (s >= send)
    goto done;
  switch (c=*s) {
  case 'D':
  case 'd':
  case 'E':
  case 'e': s++; break;
  }
  if (s >= send)
    goto done;
  switch (c=*s) {
  case '+':
  case '-': *t++ = c; s++; break;
  }
 edigits0:
  if (s >= send)
    goto done;
  switch (c=*s) {
  case '0' ... '9': *t++ = c; s++; edigits++; goto edigits0;
  default: goto error;
  }
 done:
  if (edigits == 0)
    *t++ = '0';
  *t++ = '\0';
  assert(t-cnum <= u+3);
  r = strtod(cnum, &endconv);
  assert(*endconv == '\0');
  *rp = r;
  return -1;
 return0:
  *rp = 0.0;
  return -1;
 error:
  *rp = 0.0;
  return 0;
}
#endif

Floating-Point Words

Bare FPU Words (Without C Math Library)

f+      ( r1 r2 -- r3 )     Add r1 to r2 giving the sum r3
f-      ( r1 r2 -- r3 )     Subtract r2 from r1, giving r3
f*      ( r1 r2 -- r3 )     Multiply r1 by r2 giving r3
f/      ( r1 r2 -- r3 )     Divide r1 by r2, giving the quotient r3
fsqrt   ( r1 -- r2 )        r2 is the square root of r1

fabs    ( r1 -- r2 )        r2 is the absolute value of r1
fnegate ( r1 -- r2 )        r2 is the negation of r1
fround  ( r1 -- r2 )        round r1 to an integral value using the "round to nearest" rule, giving r2

fflags@ ( -- u )            get the current value of the Floating Point Status/Control register FPSCR
fflags! ( u -- )            assign the given value to the Floating Point Status/Control register FPSCR

f0=     ( r -- ? )          flag is true if r is equal to zero
f0<     ( r -- ? )          flag is true if r is less than zero
f<      ( r1 r2 -- ? )      flag is true if r1 is less than r2
f~      ( r1 r2 r3 -- ? )   If r3 is positive, flag is true if the absolute value of (r1 minus r2) is less than r3
                            If r3 is zero, flag is true if the implementation-dependent encoding of r1 and r2 are exactly identical 
                             (positive and negative zero are unequal if they have distinct encodings).
                            If r3 is negative, flag is true if the absolute value of (r1 minus r2) is less than the absolute value 
                            of r3 times the sum of the absolute values of r1 and r2. 

f>s     ( r -- n )          n is the single-cell signed-integer equivalent of the integer portion of r
s>f     ( n -- r )          r is the floating-point equivalent of the single-cell value n
f>fx    ( r -- d )          d is the fixed-point equivalent of the floating-point r
fx>f    ( d -- r )          r is the floating-point equivalent of the fixed-point d

pi      (  -- r )           r is pi, approx. 3.14159274101257324

fnumber (a # -- r u )       convert the numbered string to float r, on success u is 1, fail 0
>float  (a # -- r ? )       convert the specified string by a and # to float r, on success flag is true (more robust)

f.            ( r --  )     display, with a trailing space, the floating-point number r in fixed-point notation
fe.           ( r --  )     display, with a trailing space, the floating-point number r in engineering notation
fs.           ( r --  )     display, with a trailing space, the floating-point number r in scientific notation
precision     ( -- u )      return the number of significant digits currently used by F., FE., or FS. as u
set-precision ( u -- )      set the number of significant digits currently used by F., FE., or FS. to u

Fixed-Point Words

d+      ( d1 d2 -- d3 )     add d1 to d2 giving the sum d3
d-      ( d1 d2 -- d3 )     subtract d2 from d1, giving d3
fx*     ( d1 d2 -- d3 )     multiply d1 by d2 giving d3
fx/     ( d1 d2 -- d3 )     divide d1 by d2, giving the quotient d3
fx.     ( d --  )           display, with a trailing space, the fixed-point number d
fx.n 	( d n -- ) 	    print a fixed-point number with n fractional digits (truncated)
f#S 	( n1 -- n2 ) 	    Adds 32 comma-digits to number output
f# 	( n1 -- n2 ) 	    Adds one comma-digit to number output

Words Using C Math Library

fsin    ( r1 -- r2 )       r2 is the sine of the radian angle r1