Why Floating-Point?

STM AN4044: One alternative to floating-point is fixed-point, where the exponent field is fixed. But if fixed-point is giving better calculation speed on FPU-less processors, the range of numbers and their dynamic is low. As a consequence, a developer using the fixed-point technique will have to check carefully any scaling/saturation issues in the algorithm.

Floating-Point Unit

Also from STM AN4044

Floating-point calculations require a lot of resources, as for any operation between two numbers. For example, we need to:

• Align the two numbers (have them with the same exponent)
• Perform the operation
• Round out the result
• Code the result

On an FPU-less processor, all these operations are done by software through the C compiler library (or Forth Words) and are not visible to the programmer; but the performances are very low. On a processor having an FPU, all of the operations are entirely done by hardware in a single cycle, for most of the instructions. The C (or Forth) compiler does not use its own floating-point library but directly generates FPU native instructions.

When implementing a mathematical algorithm on a microprocessor having an FPU, the programmer does not have to choose between performance and development time. The FPU brings reliability allowing to use directly any generated code through a high level tool, such as MATLAB or Scilab, with the highest level of performance.

Any integer with absolute value less than 2^24 can be exactly represented in the single-precision format, and any integer with absolute value less than 2^53 can be exactly represented in the double-precision format.

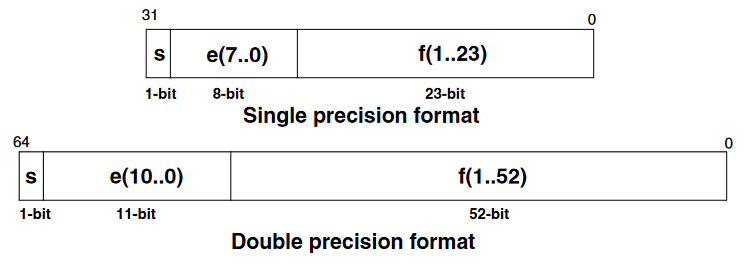
Normalized Numbers Range

IEEE.754 Single and Double Precision Floating-Point Coding

FPU's Dark Corners

Some Links

• https://forth-standard.org/standard/float
• https://de.wikipedia.org/wiki/IEEE_754
• Fixed Point

• https://www.complang.tuwien.ac.at/forth/gforth/Docs-html/Number-Conversion.html#Number-Conversion
• https://www.complang.tuwien.ac.at/forth/gforth/Docs-html/Floating-Point.html#Floating-Point
• https://forth-standard.org/proposals/recognizer#contribution-142
• https://interrupt.memfault.com/blog/cortex-m-rtos-context-switching ARM Cortex-M RTOS Context Switching
• printf("%f", myFloat) f. fe. fs.
• atof() oder strtof() benutzen?

• nur single-precision? (7..8 Dezimalstellen, H7 hat double precision FPU)
• kein eigener Stack
• auf float in ISR verzichten
• _FPU_USED

>float in Gforth engine/support.c verwendet strtod() (strtof() for single precision)

Cell to_float(Char *c_addr, UCell u, Float *rp)
{
  /* convertible string := <significand>[<exponent>]
     <significand> := [<sign>]{<digits>[.<digits0>] | .<digits> }
     <exponent>    := <marker><digits0>
     <marker>      := {<e-form> | <sign-form>}
     <e-form>      := <e-char>[<sign-form>]
     <sign-form>   := { + | - }
     <e-char>      := { D | d | E | e }
  */
  Char *s = c_addr;
  Char c;
  Char *send = c_addr+u;
  UCell ndigits = 0;
  UCell ndots = 0;
  UCell edigits = 0;
  char cnum[u+3]; /* append at most "e0\0" */
  char *t=cnum;
  char *endconv;
  Float r;
  
  if (s >= send) /* treat empty string as 0e */
    goto return0;
  switch ((c=*s)) {
  case ' ':
    /* "A string of blanks should be treated as a special case
       representing zero."*/
    for (s++; s<send; )
      if (*s++ != ' ')
        goto error;
    goto return0;
  case '-':
  case '+': *t++ = c; s++; goto aftersign;
  }
  aftersign: 
  if (s >= send)
    goto exponent;
  switch (c=*s) {
  case '0' ... '9': *t++ = c; ndigits++; s++; goto aftersign;
  case '.':         *t++ = c; ndots++;   s++; goto aftersign;
  default:                                    goto exponent;
  }
 exponent:
  if (ndigits < 1 || ndots > 1)
    goto error;
  *t++ = 'E';
  if (s >= send)
    goto done;
  switch (c=*s) {
  case 'D':
  case 'd':
  case 'E':
  case 'e': s++; break;
  }
  if (s >= send)
    goto done;
  switch (c=*s) {
  case '+':
  case '-': *t++ = c; s++; break;
  }
 edigits0:
  if (s >= send)
    goto done;
  switch (c=*s) {
  case '0' ... '9': *t++ = c; s++; edigits++; goto edigits0;
  default: goto error;
  }
 done:
  if (edigits == 0)
    *t++ = '0';
  *t++ = '\0';
  assert(t-cnum <= u+3);
  r = strtod(cnum, &endconv);
  assert(*endconv == '\0');
  *rp = r;
  return -1;
 return0:
  *rp = 0.0;
  return -1;
 error:
  *rp = 0.0;
  return 0;
}
#endif

Floating-Point Words

Bare FPU Words (Without C Math Library)

f+      ( r1 r2 -- r3 )     Add r1 to r2 giving the sum r3.
f-      ( r1 r2 -- r3 )     Subtract r2 from r1, giving r3.
f*      ( r1 r2 -- r3 )     Multiply r1 by r2 giving r3.
f/      ( r1 r2 -- r3 )     Divide r1 by r2, giving the quotient r3.
fsqrt   ( r1 -- r2 )        r2 is the square root of r1.
fabs    ( r1 -- r2 )        r2 is the absolute value of r1.
fnegate ( r1 -- r2 )        r2 is the negation of r1.

f0=     ( r -- ? )          flag is true if and only if r is equal to zero
f0<     ( r -- ? )          flag is true if and only if r is less than zero
f<      ( r1 r2 -- ? )      flag is true if and only if r1 is less than r2
f~      ( r1 r2 r3 -- ? )   If r3 is positive, flag is true if the absolute value of (r1 minus r2) is less than r3
                            If r3 is zero, flag is true if the implementation-dependent encoding of r1 and r2 are exactly identical 
                             (positive and negative zero are unequal if they have distinct encodings).
                            If r3 is negative, flag is true if the absolute value of (r1 minus r2) is less than the absolute value 
                            of r3 times the sum of the absolute values of r1 and r2. 

f>s     ( r -- n )          n is the single-cell signed-integer equivalent of the integer portion of r.
s>f     ( n -- r )          r is the floating-point equivalent of the single-cell value n.
f>fx    ( r -- d )          d is the fixed-point equivalent of the floating-point r
fx>f    ( d -- r )          r is the floating-point equivalent of the fixed-point d.

f.      ( r --  )           Display, with a trailing space, the top number using fixed-point notation:

fx*
fx/

Words Using C Math Library

fsin    ( r1 -- r2 )       r2 is the sine of the radian angle r1