
Difference: FloatingPointUnit (1 vs. 44)
Revision 442022-12-30 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 9 to 9 | ||||||||
| Added: | ||||||||
| > > | ||||||||
| STM AN4044 | ||||||||
| Line: 24 to 27 | ||||||||
| Added: | ||||||||
| > > | https://www.jostbuergi.com | |||||||
| Line: 473 to 478 | ||||||||
| ||||||||
| Added: | ||||||||
| > > |
| |||||||
Revision 432022-12-03 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 130 to 130 | ||||||||
| fnegate ( r1 -- r2 ) r2 is the negation of r1 fround ( r1 -- r2 ) round r1 to an integral value using the "round to nearest" rule, giving r2 floor ( r1 -- r2 ) round r1 to an integral value using the "round toward negative infinity" rule, giving r2 | ||||||||
| Added: | ||||||||
| > > | ftrunc ( r1 -- r2 ) round r1 to an integral value using the "round towards zero" rule, giving r2. | |||||||
| 10**>f ( n -- r ) raise 10 to the power n, giving product r flog>n ( r -- n ) n is the base-ten logarithm of r | ||||||||
Revision 422022-12-03 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 129 to 129 | ||||||||
| fabs ( r1 -- r2 ) r2 is the absolute value of r1 fnegate ( r1 -- r2 ) r2 is the negation of r1 fround ( r1 -- r2 ) round r1 to an integral value using the "round to nearest" rule, giving r2 | ||||||||
| Added: | ||||||||
| > > | floor ( r1 -- r2 ) round r1 to an integral value using the "round toward negative infinity" rule, giving r2 | |||||||
| 10**>f ( n -- r ) raise 10 to the power n, giving product r flog>n ( r -- n ) n is the base-ten logarithm of r | ||||||||
| Line: 176 to 177 | ||||||||
| fasin ( r1 -- r2 ) r2 is the principal radian angle whose sine is r1 facos ( r1 -- r2 ) r2 is the principal radian angle whose cosine is r1 fatan ( r1 -- r2 ) r2 is the principal radian angle whose tangent is r1 | ||||||||
| Added: | ||||||||
| > > | fsincos ( r1 -- r2 r3 ) r2 is the sine of the radian angle r1. r3 is the cosine of the radian angle r1 fatan2 ( r1 r2 -- r3 ) r3 is the principal radian angle (between -π and π) whose tangent is r1/r2 | |||||||
| fsinh ( r1 -- r2 ) r2 is the hyperbolic sine of r1 fcosh ( r1 -- r2 ) r2 is the hyperbolic cosine of r1 | ||||||||
Revision 412022-12-01 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 166 to 166 | ||||||||
|
Words Using the C Math Library | ||||||||
| Changed: | ||||||||
| < < | C mathematical functions | |||||||
| > > |
FPU support without trigonometric, hyperbolic and exponential functions is not even half the battle. Fortunately there is the GNU C math library. C mathematical functions | |||||||
fsin ( r1 -- r2 ) r2 is the sine of the radian angle r1 | ||||||||
| Line: 261 to 262 | ||||||||
|
RC time constant | ||||||||
| Changed: | ||||||||
| < < | 2.2n 47k f* fm. 103u ok. | |||||||
| > > | 2.2n 47k f* dup fm. 103u ok.
cutoff frequency2e pi f* f* 1e swap f/ fm. 1.54k ok. | |||||||
| Changed: | ||||||||
| < < | Mecrisp-Cube has the word f. defined as an assembler routine in fpu.s | |||||||
| > > | Mecrisp-Cube has the word f. defined as an assembler routine in fpu.s | |||||||
: f. ( r -- ) \ display, with a trailing space, the floating-point number r in fixed-point notation dup f0< if | ||||||||
Revision 402022-11-22 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 300 to 300 | ||||||||
Simple test program to estimate execution time of fsin and fsqrt:
| ||||||||
| Changed: | ||||||||
| < < | : test ( -- n ) \ test 1000 times sin return n in ms | |||||||
| > > | : test-fpu ( -- n ) \ test 1000 times sin return n in ms | |||||||
| osKernelGetTickCount cr pi 2e f* 1000e f/ \ 2*pi/1000 cr | ||||||||
Revision 392022-11-20 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 296 to 296 | ||||||||
Performance Estimation | ||||||||
| Changed: | ||||||||
| < < | All measurements and calculation are based on the Cortex M4F MCU STM32WB55 @ 32 MHz. | |||||||
| > > | All measurements and calculation are based on the Cortex M4F MCU STM32WB55 @ 32 MHz. | |||||||
Simple test program to estimate execution time of fsin and fsqrt:
| ||||||||
| Line: 315 to 315 | ||||||||
| ; | ||||||||
| Changed: | ||||||||
| < < | With fsin it takes about 7 ms, without about 1 ms for 1000 iterations. Therefore a fsin word takes about 6 us. | |||||||
| > > | With fsin it takes about 7 ms, without about 1 ms for 1000 iterations. Therefore a fsin word takes about 6 us. For the !STM32F405 @ 168 MHz, the fsin takes about 2 us. | |||||||
| Changed: | ||||||||
| < < | fsqrt takes also about 2 ms for 1000 iterations. Therefore a fsin word takes about 1 us or less. | |||||||
| > > | fsqrt takes also about 2 ms for 1000 iterations. Therefore a fsqrt word takes about 1 us or less (the same time as f/, see below). | |||||||
Basic operations like f/ are defined as inline. First check fsin and f/ with the builtin disassembler:
| ||||||||
Revision 382022-11-20 - PeterSchmid
Revision 372022-11-19 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 93 to 93 | ||||||||
| Changed: | ||||||||
| < < | Some Links | |||||||
| > > | Links | |||||||
| Line: 213 to 213 | ||||||||
| x.n ( r n -- ) print a fixed-point number r with n fractional digits (truncated) x#S ( n1 -- n2 ) Adds 32 comma-digits to number output x# ( n1 -- n2 ) Adds one comma-digit to number output | ||||||||
| Deleted: | ||||||||
| < < | d>s s>d | |||||||
|
Words from fixpt-mat-lib.fs | ||||||||
| Line: 308 to 305 | ||||||||
| pi 2e f* 1000e f/ \ 2*pi/1000 cr 1000 0 do | ||||||||
| Changed: | ||||||||
| < < | dup i s>f f* drop \ dup i s>f f* fsin drop | |||||||
| > > | \ dup i s>f f* drop dup i s>f f* fsin drop | |||||||
| \ i . dup i s>f f* fsin fs. cr \ i . dup i s>f f* fsin hex. cr loop | ||||||||
| Line: 387 to 384 | ||||||||
| 323 | ||||||||
| Changed: | ||||||||
| < < | With sqrt it takes about 323 ms, without about 6 ms. Therefore a sqrt word takes about 317 us, with FPU it takes less than 1 us. A simple multiplication about 6 us (FPU 300 ns). | |||||||
| > > | With sqrt it takes about 323 ms (sin is not working for me), without about 6 ms. Therefore a sqrt word takes about 317 us, with FPU it takes less than 1 us. A simple multiplication about 6 us (FPU 300 ns). | |||||||
|
Only addition and subtraction are comparable:
| ||||||||
Revision 362022-11-18 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 81 to 81 | ||||||||
| ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
| |||||||
0.1005e fs. 1.01E-1 ok. 0.1005e fm. 101m ok. | ||||||||
| Line: 107 to 107 | ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > |
| |||||||
| Line: 411 to 412 | ||||||||
| vmov tos, s0 1 bx lr Cycles 5 | ||||||||
| Added: | ||||||||
| > > | ||||||||
| Added: | ||||||||
| > > | Swift-Forth on a 64 bit Windows PC @ 3.4 GHz, HW FPU
: test ( -- ) \ test 1'000 times sin, displays time in us
ucounter cr
pi 2e f* 1000e f/ \ 2*pi/1000
cr
1000 0 do
fdup i s>f f* fdrop
\ fdup i s>f f* fsin fdrop
\ i . fdup i s>f f* fsin fs. cr
\ i . fdup i s>f f* fsin hex. hex. cr
loop
fdrop
utimer
;
| |||||||
| Added: | ||||||||
| > > | 91 us, 28 us -> 63 ns for fsin. 2 magnitudes faster than Mecrisp-Cube M4F @ 32 MHz | |||||||
Conclusion | ||||||||
Revision 352022-11-17 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 152 to 152 | ||||||||
| pi ( -- r ) r is pi, approx. 3.14159274101257324 e ( -- r ) r is e, approx. 2.7182818 | ||||||||
| Added: | ||||||||
| > > | fnumber (a # -- r u ) convert the specified string by a and # to float r, on success u is 1, otherwise 0
>float (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true | |||||||
| f. ( r -- ) display, with a trailing space, the floating-point number r in fixed-point notation fs. ( r -- ) display, with a trailing space, the floating-point number r in scientific notation fe. ( r -- ) display, with a trailing space, the floating-point number r in engineering notation | ||||||||
| Line: 165 to 168 | ||||||||
| C mathematical functions
| ||||||||
| Deleted: | ||||||||
| < < | fnumber (a # -- r u ) convert the specified string by a and # to float r, on success u is 1, otherwise 0
>float (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true (more robust) | |||||||
| fsin ( r1 -- r2 ) r2 is the sine of the radian angle r1 fcos ( r1 -- r2 ) r2 is the cosine of the radian angle r1 ftan ( r1 -- r2 ) r2 is the principal radian angle whose tangent is r1 | ||||||||
| Line: 252 to 252 | ||||||||
How to Use | ||||||||
| Added: | ||||||||
| > > | Calculation of two parallel resistors | |||||||
: f|| ( r1 r2 -- r3) 2dup f* -rot f+ f/ ; 27k 100k f|| fm. 21.3k ok. | ||||||||
| Deleted: | ||||||||
| < < | 2.2n 47k f* fm. 103u ok. | |||||||
| Added: | ||||||||
| > > | RC time constant2.2n 47k f* fm. 103u ok. | |||||||
| Added: | ||||||||
| > > | Mecrisp-Cube has the word f. defined as an assembler routine in fpu.s | |||||||
: f. ( r -- ) \ display, with a trailing space, the floating-point number r in fixed-point notation dup f0< if | ||||||||
Revision 342022-11-17 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 129 to 129 | ||||||||
| fnegate ( r1 -- r2 ) r2 is the negation of r1 fround ( r1 -- r2 ) round r1 to an integral value using the "round to nearest" rule, giving r2 | ||||||||
| Added: | ||||||||
| > > | 10**>f ( n -- r ) raise 10 to the power n, giving product r flog>n ( r -- n ) n is the base-ten logarithm of r | |||||||
| fflags@ ( -- u ) get the current value of the Floating Point Status/Control register FPSCR fflags! ( u -- ) assign the given value to the Floating Point Status/Control register FPSCR | ||||||||
| Line: 150 to 153 | ||||||||
| e ( -- r ) r is e, approx. 2.7182818
f. ( r -- ) display, with a trailing space, the floating-point number r in fixed-point notation | ||||||||
| Changed: | ||||||||
| < < | precision ( -- u ) return the number of significant digits currently used by F., FE., or FS. as u set-precision ( u -- ) set the number of significant digits currently used by F., FE., or FS. to u | |||||||
| > > | fs. ( r -- ) display, with a trailing space, the floating-point number r in scientific notation fe. ( r -- ) display, with a trailing space, the floating-point number r in engineering notation fm. ( r -- ) display, with a trailing space, the floating-point number r in metric unit prefix notation precision ( -- u ) return the number of significant digits currently used by f., fs., fe., or fm. as u set-precision ( u -- ) set the number of significant digits currently used by f., fs., fe., or fm. to u | |||||||
| Line: 162 to 168 | ||||||||
| fnumber (a # -- r u ) convert the specified string by a and # to float r, on success u is 1, otherwise 0
>float (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true (more robust) | ||||||||
| Deleted: | ||||||||
| < < | fs. ( r -- ) display, with a trailing space, the floating-point number r in scientific notation fe. ( r -- ) display, with a trailing space, the floating-point number r in engineering notation fm. ( r -- ) display, with a trailing space, the floating-point number r in metric unit prefix notation | |||||||
| fsin ( r1 -- r2 ) r2 is the sine of the radian angle r1 fcos ( r1 -- r2 ) r2 is the cosine of the radian angle r1 ftan ( r1 -- r2 ) r2 is the principal radian angle whose tangent is r1 | ||||||||
Revision 332022-11-17 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 205 to 205 | ||||||||
| d- ( r1 r2 -- r3 ) subtract r2 from r1, giving r3 x* ( r1 r2 -- r3 ) multiply r1 by r2 giving r3 x/ ( r1 r2 -- r3 ) divide r1 by r2, giving the quotient r3 | ||||||||
| Added: | ||||||||
| > > | ||||||||
| x. ( r -- ) display, with a trailing space, the fixed-point number r x.n ( r n -- ) print a fixed-point number r with n fractional digits (truncated) x#S ( n1 -- n2 ) Adds 32 comma-digits to number output x# ( n1 -- n2 ) Adds one comma-digit to number output | ||||||||
| Added: | ||||||||
| > > | d>s
s>d
Words from fixpt-mat-lib.fs | |||||||
| sqrt ( r1 -- r2 ) r2 is the square root of r1 sin cos | ||||||||
| Line: 234 to 241 | ||||||||
| +inf -inf | ||||||||
| Deleted: | ||||||||
| < < | *) fixpt-mat-lib.fs | |||||||
| Line: 250 to 256 | ||||||||
| ;
27k 100k f|| fm. 21.3k ok. | ||||||||
| Added: | ||||||||
| > > | 2.2n 47k f* fm. 103u ok. | |||||||
|
: f. ( r -- ) \ display, with a trailing space, the floating-point number r in fixed-point notation | ||||||||
| Added: | ||||||||
| > > | dup f0< if 45 emit fabs then dup | |||||||
| $3F000000 \ .5 precision 0 do $41200000 f/ \ 10.0 / | ||||||||
| Line: 279 to 291 | ||||||||
Performance Estimation | ||||||||
| Changed: | ||||||||
| < < | STM32WB @ 32 MHz | |||||||
| > > | All measurements and calculation are based on the Cortex M4F MCU STM32WB55 @ 32 MHz.
Simple test program to estimate execution time of | |||||||
: test ( -- n ) \ test 1000 times sin return n in ms osKernelGetTickCount cr | ||||||||
| Line: 296 to 310 | ||||||||
| ; | ||||||||
| Changed: | ||||||||
| < < | With fsin it takes about 7 ms, without about 1 ms. Therefore a fsin word takes about 6 us. | |||||||
| > > | With fsin it takes about 7 ms, without about 1 ms for 1000 iterations. Therefore a fsin word takes about 6 us.
| |||||||
Basic operations like f/ are defined as inline. First check fsin and f/ with the builtin disassembler:
| ||||||||
| Line: 336 to 352 | ||||||||
| vdiv.f32 s0, s0, s1 14 vmov tos, s0 1 bx lr | ||||||||
| Added: | ||||||||
| > > | cycles 18
About 20 cycles (625 ns @ 32 MHz) for a division, 10 (300 ns) for multiplication, and 5 (150 ns) for +/-. vsqrt.f32 has 14 cycles. | |||||||
| Added: | ||||||||
| > > | include /fsr/fixpt-math-lib.fs ok.
: test-fix ( -- n ) \ test 1000 times fixed-point sin return n in ms
osKernelGetTickCount cr
\ pi 2e f* 1000e f/ \ 2*pi/1000
360,0 1000,0 x/
cr
1000 0 do
\ 2dup i 0 swap x* 2drop
\ 2dup i 0 swap x* sin 2drop
2dup i 0 swap x* sqrt 2drop
\ i . 2dup i 0 swap x* sin x. cr
\ i . 2dup i 0 swap x* sqrt x. cr
\ i . 2dup i 0 swap x* sin hex. hex. cr
loop
2drop
osKernelGetTickCount swap -
;
test-fix .
323
| |||||||
| Changed: | ||||||||
| < < | About 20 cycles (625 ns @ 32 MHz) for a division, 10 (300 ns) for multiplication, and 5 (150 ns) for +/-. | |||||||
| > > | With sqrt it takes about 323 ms, without about 6 ms. Therefore a sqrt word takes about 317 us, with FPU it takes less than 1 us. A simple multiplication about 6 us (FPU 300 ns).
Only addition and subtraction are comparable: see d+
080008B6: CF07 ldmia r7 { r0 r1 r2 } 1
080008B8: 1812 adds r2 r2 r0 1
080008BA: 414E adcs r6 r1 1
080008BC: 3F04 subs r7 #4 1
080008BE: 603A str r2 [ r7 #0 ] 1
080008C0: 4770 bx lr
Cycles 5
| |||||||
| Added: | ||||||||
| > > | @ -----------------------------------------------------------------------------
Wortbirne Flag_foldable_2|Flag_inline, "f+"
f_add:
@ ( r1 r2 -- r3 ) Add r1 to r2 giving the sum r3.
@ -----------------------------------------------------------------------------
vmov s1, tos 1
drop 1
vmov s0, tos 1
vadd.f32 s0, s1 1
vmov tos, s0 1
bx lr
Cycles 5
ConclusionAs long as you do only elementary arithmetic, fixed- and floating-point have comparable execution time (but division and multiplication is a magnitude slower). But for more elaborate calculation (trigonomteric, exponential functions) the execution time is for fixed-point at least two magnitudes slower. If time is not an issue in either development or execution, you can easily do without the FPU. | |||||||
| Added: | ||||||||
| > > | ||||||||
Revision 322022-11-16 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 274 to 274 | ||||||||
|
| ||||||||
| Added: | ||||||||
| > > |
Performance EstimationSTM32WB @ 32 MHz : test ( -- n ) \ test 1000 times sin return n in ms
osKernelGetTickCount cr
pi 2e f* 1000e f/ \ 2*pi/1000
cr
1000 0 do
dup i s>f f* drop
\ dup i s>f f* fsin drop
\ i . dup i s>f f* fsin fs. cr
\ i . dup i s>f f* fsin hex. cr
loop
drop
osKernelGetTickCount swap -
;
With
Basic operations like see fsin
08007BE8: B500 push { lr }
08007BEA: 4630 mov r0 r6
08007BEC: F025 bl 0802D694
08007BEE: FD52
08007BF0: 4606 mov r6 r0
08007BF2: BD00 pop { pc }
ok.
The FPU instructions are unknown to the disassembler
see f/
0800745A: EE00
0800745C: 6A90
0800745E: CF40 ldmia r7 { r6 }
08007460: EE00
08007462: 6A10
08007464: EE80
08007466: 0A20
08007468: EE10
0800746A: 6A10
0800746C: 4770 bx lr
From fpu.s@ -----------------------------------------------------------------------------
Wortbirne Flag_foldable_2|Flag_inline, "f/"
f_slash:
@ ( r1 r2 -- r3 ) Divide r1 by r2, giving the quotient r3.
@ -----------------------------------------------------------------------------
vmov s1, tos 1
drop ldmia r7 { r6 } 1
vmov s0, tos 1
vdiv.f32 s0, s0, s1 14
vmov tos, s0 1
bx lr
About 20 cycles (625 ns @ 32 MHz) for a division, 10 (300 ns) for multiplication, and 5 (150 ns) for +/-.
| |||||||
Revision 312022-11-16 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 21 to 21 | ||||||||
| ||||||||
| Added: | ||||||||
| > > | ||||||||
|
Contents
| ||||||||
| Line: 154 to 156 | ||||||||
|
Words Using the C Math Library | ||||||||
| Added: | ||||||||
| > > | C mathematical functions | |||||||
fnumber (a # -- r u ) convert the specified string by a and # to float r, on success u is 1, otherwise 0 | ||||||||
Revision 302022-11-15 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 79 to 79 | ||||||||
| ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
| |||||||
0.1005e fs. 1.01E-1 ok. 0.1005e fm. 101m ok. 4 set-precision 0.100005e fs. 1.0000E-1 ok. 0.100005e fm. 100.00m ok. | ||||||||
| Added: | ||||||||
| > > | 1.00005e f>x x. 1,00004994869232177734375000000000 ok. 1,00005 x. 1,00004999991506338119506835937500 ok. | |||||||
| Line: 238 to 240 | ||||||||
| Added: | ||||||||
| > > |
| |||||||
| : f|| ( r1 r2 -- r3) | ||||||||
| Changed: | ||||||||
| < < | 2dup * -rot + / | |||||||
| > > | 2dup f* -rot f+ f/ | |||||||
| ; | ||||||||
| Changed: | ||||||||
| < < | 27k 100k f|| fm. | |||||||
| > > | 27k 100k f|| fm. 21.3k ok.
: f. ( r -- ) \ display, with a trailing space, the floating-point number r in fixed-point notation
$3F000000 \ .5
precision 0 do
$41200000 f/ \ 10.0 /
loop
f+ \ round
f>x
<#
0 #s 2drop \ integer part
46 hold< \ decimal point
precision 0 do
x# \ fract digit
loop
dup
#>
type space
;
| |||||||
Revision 292022-11-14 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 75 to 75 | ||||||||
Some Hints for Using the FPU | ||||||||
| Changed: | ||||||||
| < < | It is better to be approximately right than exactly wrong. | |||||||
| > > | It is better to be approximately (vaguely) right than exactly wrong. Carveth Read | |||||||
| ||||||||
| Line: 95 to 95 | ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > | ||||||||
| Line: 232 to 232 | ||||||||
| *) fixpt-mat-lib.fs | ||||||||
| Added: | ||||||||
| > > |
| |||||||
Revision 282022-11-14 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 75 to 75 | ||||||||
Some Hints for Using the FPU | ||||||||
| Changed: | ||||||||
| < < | Rounding is not very useful for precision more than 3. | |||||||
| > > | It is better to be approximately right than exactly wrong.
| |||||||
0.1005e fs. 1.01E-1 ok. 0.1005e fm. 101m ok. | ||||||||
| Line: 84 to 88 | ||||||||
| 0.100005e fm. 100.00m ok. | ||||||||
| Deleted: | ||||||||
| < < | Do not use FPU in interrupt service routines.
Tasks/Threads with FPU operations need much more return stack depth. | |||||||
Some Links
| ||||||||
| Added: | ||||||||
| > > | ||||||||
|
| ||||||||
Revision 272022-11-13 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 72 to 72 | ||||||||
| Changed: | ||||||||
| < < | FPU's Dark Corners | |||||||
| > > |
Some Hints for Using the FPURounding is not very useful for precision more than 3. 0.1005e fs. 1.01E-1 ok. 0.1005e fm. 101m ok. 4 set-precision 0.100005e fs. 1.0000E-1 ok. 0.100005e fm. 100.00m ok. Do not use FPU in interrupt service routines. Tasks/Threads with FPU operations need much more return stack depth. | |||||||
Some Links | ||||||||
Revision 262022-11-12 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 180 to 180 | ||||||||
|
All angles are in degrees.
| ||||||||
| Changed: | ||||||||
| < < | d+ ( x1 x2 -- x3 ) add x1 to x2 giving the sum x3 d- ( x1 x2 -- x3 ) subtract x2 from x1, giving x3 x* ( x1 x2 -- x3 ) multiply x1 by x2 giving x3 x/ ( x1 x2 -- x3 ) divide x1 by x2, giving the quotient x3 x. ( x -- ) display, with a trailing space, the fixed-point number x x.n ( x n -- ) print a fixed-point number x with n fractional digits (truncated) | |||||||
| > > | d+ ( r1 r2 -- r3 ) add r1 to r2 giving the sum r3 d- ( r1 r2 -- r3 ) subtract r2 from r1, giving r3 x* ( r1 r2 -- r3 ) multiply r1 by r2 giving r3 x/ ( r1 r2 -- r3 ) divide r1 by r2, giving the quotient r3 x. ( r -- ) display, with a trailing space, the fixed-point number r x.n ( r n -- ) print a fixed-point number r with n fractional digits (truncated) | |||||||
| x#S ( n1 -- n2 ) Adds 32 comma-digits to number output x# ( n1 -- n2 ) Adds one comma-digit to number output | ||||||||
| Changed: | ||||||||
| < < | sqrt ( x1 -- x2 ) x2 is the square root of x1 | |||||||
| > > | sqrt ( r1 -- r2 ) r2 is the square root of r1 | |||||||
| sin cos tan | ||||||||
Revision 252022-11-12 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 68 to 68 | ||||||||
 | ||||||||
| Added: | ||||||||
| > > | ||||||||
FPU's Dark Corners
Some Links | ||||||||
| Line: 137 to 141 | ||||||||
| fnumber (a # -- r u ) convert the specified string by a and # to float r, on success u is 1, otherwise 0
>float (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true (more robust) | ||||||||
| Deleted: | ||||||||
| < < | fe. ( r -- ) display, with a trailing space, the floating-point number r in engineering notation | |||||||
| fs. ( r -- ) display, with a trailing space, the floating-point number r in scientific notation | ||||||||
| Changed: | ||||||||
| < < | fu. ( r -- ) display, with a trailing space, the floating-point number r in (metric) unit prefix notation | |||||||
| > > | fe. ( r -- ) display, with a trailing space, the floating-point number r in engineering notation fm. ( r -- ) display, with a trailing space, the floating-point number r in metric unit prefix notation | |||||||
| fsin ( r1 -- r2 ) r2 is the sine of the radian angle r1 fcos ( r1 -- r2 ) r2 is the cosine of the radian angle r1 | ||||||||
Revision 242022-11-11 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 125 to 125 | ||||||||
| pi ( -- r ) r is pi, approx. 3.14159274101257324 e ( -- r ) r is e, approx. 2.7182818 | ||||||||
| Deleted: | ||||||||
| < < | fnumber (a # -- r u ) convert the specified string by a and # to float r, on success u is 1, otherwise 0
>float (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true (more robust) | |||||||
| f. ( r -- ) display, with a trailing space, the floating-point number r in fixed-point notation | ||||||||
| Deleted: | ||||||||
| < < | fe. ( r -- ) display, with a trailing space, the floating-point number r in engineering notation fs. ( r -- ) display, with a trailing space, the floating-point number r in scientific notation fu. ( r -- ) display, with a trailing space, the floating-point number r in unit (metric) prefix notation | |||||||
| precision ( -- u ) return the number of significant digits currently used by F., FE., or FS. as u set-precision ( u -- ) set the number of significant digits currently used by F., FE., or FS. to u | ||||||||
| Changed: | ||||||||
| < < | Words Using C Math Library | |||||||
| > > | Words Using the C Math Library | |||||||
|
| ||||||||
| Added: | ||||||||
| > > | fnumber (a # -- r u ) convert the specified string by a and # to float r, on success u is 1, otherwise 0
>float (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true (more robust) fe. ( r -- ) display, with a trailing space, the floating-point number r in engineering notation fs. ( r -- ) display, with a trailing space, the floating-point number r in scientific notation fu. ( r -- ) display, with a trailing space, the floating-point number r in (metric) unit prefix notation | |||||||
| fsin ( r1 -- r2 ) r2 is the sine of the radian angle r1 fcos ( r1 -- r2 ) r2 is the cosine of the radian angle r1 ftan ( r1 -- r2 ) r2 is the principal radian angle whose tangent is r1 | ||||||||
| Line: 208 to 209 | ||||||||
| +inf -inf | ||||||||
| Changed: | ||||||||
| < < | fixpt-mat-lib.fs | |||||||
| > > | *) fixpt-mat-lib.fs | |||||||
|
| ||||||||
Revision 232022-11-11 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 131 to 131 | ||||||||
| f. ( r -- ) display, with a trailing space, the floating-point number r in fixed-point notation fe. ( r -- ) display, with a trailing space, the floating-point number r in engineering notation fs. ( r -- ) display, with a trailing space, the floating-point number r in scientific notation | ||||||||
| Added: | ||||||||
| > > | fu. ( r -- ) display, with a trailing space, the floating-point number r in unit (metric) prefix notation | |||||||
| precision ( -- u ) return the number of significant digits currently used by F., FE., or FS. as u set-precision ( u -- ) set the number of significant digits currently used by F., FE., or FS. to u | ||||||||
Revision 222022-11-05 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 119 to 119 | ||||||||
| f>s ( r -- n ) n is the single-cell signed-integer equivalent of the integer portion of r s>f ( n -- r ) r is the floating-point equivalent of the single-cell value n | ||||||||
| Changed: | ||||||||
| < < | f>fx ( r -- x ) x is the fixed-point equivalent of the floating-point r fx>f ( x -- r ) r is the floating-point equivalent of the fixed-point x | |||||||
| > > | f>x ( r -- x ) x is the fixed-point equivalent of the floating-point r x>f ( x -- r ) r is the floating-point equivalent of the fixed-point x | |||||||
| pi ( -- r ) r is pi, approx. 3.14159274101257324 e ( -- r ) r is e, approx. 2.7182818 | ||||||||
| Line: 136 to 136 | ||||||||
| Deleted: | ||||||||
| < < | ||||||||
Words Using C Math Library
fsin ( r1 -- r2 ) r2 is the sine of the radian angle r1 | ||||||||
| Added: | ||||||||
| > > | fcos ( r1 -- r2 ) r2 is the cosine of the radian angle r1
ftan ( r1 -- r2 ) r2 is the principal radian angle whose tangent is r1
fasin ( r1 -- r2 ) r2 is the principal radian angle whose sine is r1
facos ( r1 -- r2 ) r2 is the principal radian angle whose cosine is r1
fatan ( r1 -- r2 ) r2 is the principal radian angle whose tangent is r1
fsinh ( r1 -- r2 ) r2 is the hyperbolic sine of r1 fcosh ( r1 -- r2 ) r2 is the hyperbolic cosine of r1 ftanh ( r1 -- r2 ) r2 is the hyperbolic tangent of r1 fasinh ( r1 -- r2 ) r2 is the floating-point value whose hyperbolic sine is r1 facosh ( r1 -- r2 ) r2 is the floating-point value whose hyperbolic cosine is r1 fatanh ( r1 -- r2 ) r2 is the floating-point value whose hyperbolic tangent is r1 fceil ( r1 -- r2 ) return the smallest integral value that is not less than r1 ffloor ( r1 -- r2 ) Round r1 to an integral value using the "round toward negative infinity" rule, giving r2 fexp ( r1 -- r2 ) raise e to the power r1, giving r2. f** ( r1 r2 -- r3 ) raise r1 to the power r2, giving the product r3 fln ( r1 -- r2 ) r2 is the natural logarithm of r1 flog ( r1 -- r2 ) r2 is the base-ten logarithm of r1 | |||||||
| Added: | ||||||||
| > > | ||||||||
| Changed: | ||||||||
| < < | Fixed-Point Words | |||||||
| > > | ||||||||
|
Fixed-point | ||||||||
Revision 212022-11-05 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Changed: | ||||||||
| < < | image="/twiki/pub/Cosmac/ForthSTM32WB/nucleo-header.jpg" | |||||||
| > > | image="/twiki/pub/MecrispCube/FloatingPointUnit/Float_example-header.png" | |||||||
| title="Floating-Point Unit (FPU)" | ||||||||
| Changed: | ||||||||
| < < | titlestyle="color:#F00000;" | |||||||
| > > | titlestyle="color:#ffffff;" | |||||||
| }% | ||||||||
| Line: 29 to 29 | ||||||||
| Added: | ||||||||
| > > | The STM32 ARM Cortex M4F MPUs (e.g. STM32WB, STM32F4, STM32L4) have a single precision floating-point unit. The STM32H7 MPUs have a double precision FPU (not supported yet). | |||||||
| Also from STM AN4044 Floating-point calculations require a lot of resources, as for any operation between two | ||||||||
| Line: 61 to 63 | ||||||||
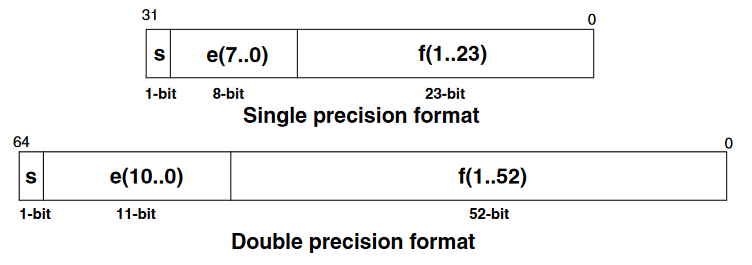
IEEE.754 Single and Double Precision Floating-Point Coding | ||||||||
| Added: | ||||||||
| > > | ||||||||

FPU's Dark Corners | ||||||||
| Line: 79 to 84 | ||||||||
| Deleted: | ||||||||
| < < |
Cell to_float(Char *c_addr, UCell u, Float *rp)
{
/* convertible string := <significand>[<exponent>]
<significand> := [<sign>]{<digits>[.<digits0>] | .<digits> }
<exponent> := <marker><digits0>
<marker> := {<e-form> | <sign-form>}
<e-form> := <e-char>[<sign-form>]
<sign-form> := { + | - }
<e-char> := { D | d | E | e }
*/
Char *s = c_addr;
Char c;
Char *send = c_addr+u;
UCell ndigits = 0;
UCell ndots = 0;
UCell edigits = 0;
char cnum[u+3]; /* append at most "e0\0" */
char *t=cnum;
char *endconv;
Float r;
if (s >= send) /* treat empty string as 0e */
goto return0;
switch ((c=*s)) {
case ' ':
/* "A string of blanks should be treated as a special case
representing zero."*/
for (s++; s<send; )
if (*s++ != ' ')
goto error;
goto return0;
case '-':
case '+': *t++ = c; s++; goto aftersign;
}
aftersign:
if (s >= send)
goto exponent;
switch (c=*s) {
case '0' ... '9': *t++ = c; ndigits++; s++; goto aftersign;
case '.': *t++ = c; ndots++; s++; goto aftersign;
default: goto exponent;
}
exponent:
if (ndigits < 1 || ndots > 1)
goto error;
*t++ = 'E';
if (s >= send)
goto done;
switch (c=*s) {
case 'D':
case 'd':
case 'E':
case 'e': s++; break;
}
if (s >= send)
goto done;
switch (c=*s) {
case '+':
case '-': *t++ = c; s++; break;
}
edigits0:
if (s >= send)
goto done;
switch (c=*s) {
case '0' ... '9': *t++ = c; s++; edigits++; goto edigits0;
default: goto error;
}
done:
if (edigits == 0)
*t++ = '0';
*t++ = '\0';
assert(t-cnum <= u+3);
r = strtod(cnum, &endconv);
assert(*endconv == '\0');
*rp = r;
return -1;
return0:
*rp = 0.0;
return -1;
error:
*rp = 0.0;
return 0;
}
#endif
| |||||||
|
| ||||||||
| Added: | ||||||||
| > > | No separate floating-point stack. A single precision floating-point number is one cell. The 32-bit base-2 format is officially referred to as binary32 IEEE 754-2008 | |||||||
Bare FPU Words (Without C Math Library)
| ||||||||
| Line: 206 to 119 | ||||||||
| f>s ( r -- n ) n is the single-cell signed-integer equivalent of the integer portion of r s>f ( n -- r ) r is the floating-point equivalent of the single-cell value n | ||||||||
| Changed: | ||||||||
| < < | f>fx ( r -- d ) d is the fixed-point equivalent of the floating-point r fx>f ( d -- r ) r is the floating-point equivalent of the fixed-point d | |||||||
| > > | f>fx ( r -- x ) x is the fixed-point equivalent of the floating-point r fx>f ( x -- r ) r is the floating-point equivalent of the fixed-point x | |||||||
| pi ( -- r ) r is pi, approx. 3.14159274101257324 e ( -- r ) r is e, approx. 2.7182818 | ||||||||
| Line: 222 to 135 | ||||||||
| set-precision ( u -- ) set the number of significant digits currently used by F., FE., or FS. to u | ||||||||
| Deleted: | ||||||||
| < < | Fixed-Point Wordsd+ ( d1 d2 -- d3 ) add d1 to d2 giving the sum d3 d- ( d1 d2 -- d3 ) subtract d2 from d1, giving d3 fx* ( d1 d2 -- d3 ) multiply d1 by d2 giving d3 fx/ ( d1 d2 -- d3 ) divide d1 by d2, giving the quotient d3 fx. ( d -- ) display, with a trailing space, the fixed-point number d fx.n ( d n -- ) print a fixed-point number with n fractional digits (truncated) fx#S ( n1 -- n2 ) Adds 32 comma-digits to number output fx# ( n1 -- n2 ) Adds one comma-digit to number output | |||||||
|
Words Using C Math Library | ||||||||
| Line: 242 to 144 | ||||||||
| Added: | ||||||||
| > > | Fixed-Point Words
Fixed-point All angles are in degrees. d+ ( x1 x2 -- x3 ) add x1 to x2 giving the sum x3 d- ( x1 x2 -- x3 ) subtract x2 from x1, giving x3 x* ( x1 x2 -- x3 ) multiply x1 by x2 giving x3 x/ ( x1 x2 -- x3 ) divide x1 by x2, giving the quotient x3 x. ( x -- ) display, with a trailing space, the fixed-point number x x.n ( x n -- ) print a fixed-point number x with n fractional digits (truncated) x#S ( n1 -- n2 ) Adds 32 comma-digits to number output x# ( n1 -- n2 ) Adds one comma-digit to number output sqrt ( x1 -- x2 ) x2 is the square root of x1 sin cos tan asin acos atan log2 log10 ln pow2 pow10 exp floor deg2rad ( deg -- rad ) rad2deg ( rad -- deg ) pi pi/2 pi/4 +inf -inf fixpt-mat-lib.fs | |||||||
|
| ||||||||
| Line: 252 to 197 | ||||||||
 This work by Peter Schmid is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
| ||||||||
| Added: | ||||||||
| > > |
| |||||||
Revision 202022-11-04 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 210 to 210 | ||||||||
| fx>f ( d -- r ) r is the floating-point equivalent of the fixed-point d
pi ( -- r ) r is pi, approx. 3.14159274101257324 | ||||||||
| Added: | ||||||||
| > > | e ( -- r ) r is e, approx. 2.7182818 | |||||||
| Changed: | ||||||||
| < < | fnumber (a # -- r u ) convert the numbered string to float r, on success u is 1, fail 0 | |||||||
| > > | fnumber (a # -- r u ) convert the specified string by a and # to float r, on success u is 1, otherwise 0 | |||||||
| >float (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true (more robust) f. ( r -- ) display, with a trailing space, the floating-point number r in fixed-point notation | ||||||||
| Line: 229 to 230 | ||||||||
| fx/ ( d1 d2 -- d3 ) divide d1 by d2, giving the quotient d3 fx. ( d -- ) display, with a trailing space, the fixed-point number d fx.n ( d n -- ) print a fixed-point number with n fractional digits (truncated) | ||||||||
| Changed: | ||||||||
| < < | f#S ( n1 -- n2 ) Adds 32 comma-digits to number output f# ( n1 -- n2 ) Adds one comma-digit to number output | |||||||
| > > | fx#S ( n1 -- n2 ) Adds 32 comma-digits to number output fx# ( n1 -- n2 ) Adds one comma-digit to number output | |||||||
Revision 192022-11-04 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 211 to 211 | ||||||||
| pi ( -- r ) r is pi, approx. 3.14159274101257324 | ||||||||
| Changed: | ||||||||
| < < | fnumber (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true | |||||||
| > > | fnumber (a # -- r u ) convert the numbered string to float r, on success u is 1, fail 0 | |||||||
| >float (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true (more robust) f. ( r -- ) display, with a trailing space, the floating-point number r in fixed-point notation | ||||||||
| Line: 229 to 229 | ||||||||
| fx/ ( d1 d2 -- d3 ) divide d1 by d2, giving the quotient d3 fx. ( d -- ) display, with a trailing space, the fixed-point number d fx.n ( d n -- ) print a fixed-point number with n fractional digits (truncated) | ||||||||
| Added: | ||||||||
| > > | f#S ( n1 -- n2 ) Adds 32 comma-digits to number output f# ( n1 -- n2 ) Adds one comma-digit to number output | |||||||
Revision 182022-11-04 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 210 to 210 | ||||||||
| fx>f ( d -- r ) r is the floating-point equivalent of the fixed-point d
pi ( -- r ) r is pi, approx. 3.14159274101257324 | ||||||||
| Deleted: | ||||||||
| < < | f. ( r -- ) display, with a trailing space, the floating-point number r using fixed-point notation | |||||||
| Added: | ||||||||
| > > | fnumber (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true
>float (a # -- r ? ) convert the specified string by a and # to float r, on success flag is true (more robust) f. ( r -- ) display, with a trailing space, the floating-point number r in fixed-point notation fe. ( r -- ) display, with a trailing space, the floating-point number r in engineering notation fs. ( r -- ) display, with a trailing space, the floating-point number r in scientific notation precision ( -- u ) return the number of significant digits currently used by F., FE., or FS. as u set-precision ( u -- ) set the number of significant digits currently used by F., FE., or FS. to u
Fixed-Point Words | |||||||
| d+ ( d1 d2 -- d3 ) add d1 to d2 giving the sum d3 d- ( d1 d2 -- d3 ) subtract d2 from d1, giving d3 fx* ( d1 d2 -- d3 ) multiply d1 by d2 giving d3 | ||||||||
Revision 172022-11-04 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 76 to 76 | ||||||||
| Added: | ||||||||
| > > | ||||||||
| ||||||||
Revision 162022-11-03 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 68 to 68 | ||||||||
Some Links
| ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > | ||||||||
|
| ||||||||
| Deleted: | ||||||||
| < < |
| |||||||
| ||||||||
| Line: 190 to 190 | ||||||||
| fround ( r1 -- r2 ) round r1 to an integral value using the "round to nearest" rule, giving r2
fflags@ ( -- u ) get the current value of the Floating Point Status/Control register FPSCR | ||||||||
| Changed: | ||||||||
| < < | fflags! ( -- u ) assign the given value to the Floating Point Status/Control register FPSCR | |||||||
| > > | fflags! ( u -- ) assign the given value to the Floating Point Status/Control register FPSCR | |||||||
| f0= ( r -- ? ) flag is true if r is equal to zero f0< ( r -- ? ) flag is true if r is less than zero | ||||||||
| Line: 206 to 206 | ||||||||
| f>fx ( r -- d ) d is the fixed-point equivalent of the floating-point r fx>f ( d -- r ) r is the floating-point equivalent of the fixed-point d | ||||||||
| Changed: | ||||||||
| < < | f. ( r -- ) Display, with a trailing space, the top number using fixed-point notation | |||||||
| > > | pi ( -- r ) r is pi, approx. 3.14159274101257324 f. ( r -- ) display, with a trailing space, the floating-point number r using fixed-point notation | |||||||
| Changed: | ||||||||
| < < | fx* fx/ | |||||||
| > > | d+ ( d1 d2 -- d3 ) add d1 to d2 giving the sum d3 d- ( d1 d2 -- d3 ) subtract d2 from d1, giving d3 fx* ( d1 d2 -- d3 ) multiply d1 by d2 giving d3 fx/ ( d1 d2 -- d3 ) divide d1 by d2, giving the quotient d3 fx. ( d -- ) display, with a trailing space, the fixed-point number d fx.n ( d n -- ) print a fixed-point number with n fractional digits (truncated) | |||||||
Revision 152022-11-03 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 179 to 179 | ||||||||
Bare FPU Words (Without C Math Library)
| ||||||||
| Changed: | ||||||||
| < < | f+ ( r1 r2 -- r3 ) Add r1 to r2 giving the sum r3.
f- ( r1 r2 -- r3 ) Subtract r2 from r1, giving r3.
f* ( r1 r2 -- r3 ) Multiply r1 by r2 giving r3.
f/ ( r1 r2 -- r3 ) Divide r1 by r2, giving the quotient r3.
fsqrt ( r1 -- r2 ) r2 is the square root of r1.
fabs ( r1 -- r2 ) r2 is the absolute value of r1.
fnegate ( r1 -- r2 ) r2 is the negation of r1.
f0= ( r -- ? ) flag is true if and only if r is equal to zero f0< ( r -- ? ) flag is true if and only if r is less than zero f< ( r1 r2 -- ? ) flag is true if and only if r1 is less than r2 | |||||||
| > > | f+ ( r1 r2 -- r3 ) Add r1 to r2 giving the sum r3
f- ( r1 r2 -- r3 ) Subtract r2 from r1, giving r3
f* ( r1 r2 -- r3 ) Multiply r1 by r2 giving r3
f/ ( r1 r2 -- r3 ) Divide r1 by r2, giving the quotient r3
fsqrt ( r1 -- r2 ) r2 is the square root of r1
fabs ( r1 -- r2 ) r2 is the absolute value of r1 fnegate ( r1 -- r2 ) r2 is the negation of r1 fround ( r1 -- r2 ) round r1 to an integral value using the "round to nearest" rule, giving r2 fflags@ ( -- u ) get the current value of the Floating Point Status/Control register FPSCR fflags! ( -- u ) assign the given value to the Floating Point Status/Control register FPSCR f0= ( r -- ? ) flag is true if r is equal to zero f0< ( r -- ? ) flag is true if r is less than zero f< ( r1 r2 -- ? ) flag is true if r1 is less than r2 | |||||||
| f~ ( r1 r2 r3 -- ? ) If r3 is positive, flag is true if the absolute value of (r1 minus r2) is less than r3 If r3 is zero, flag is true if the implementation-dependent encoding of r1 and r2 are exactly identical (positive and negative zero are unequal if they have distinct encodings). If r3 is negative, flag is true if the absolute value of (r1 minus r2) is less than the absolute value of r3 times the sum of the absolute values of r1 and r2. | ||||||||
| Changed: | ||||||||
| < < | f>s ( r -- n ) n is the single-cell signed-integer equivalent of the integer portion of r. s>f ( n -- r ) r is the floating-point equivalent of the single-cell value n. | |||||||
| > > | f>s ( r -- n ) n is the single-cell signed-integer equivalent of the integer portion of r s>f ( n -- r ) r is the floating-point equivalent of the single-cell value n | |||||||
| f>fx ( r -- d ) d is the fixed-point equivalent of the floating-point r | ||||||||
| Changed: | ||||||||
| < < | fx>f ( d -- r ) r is the floating-point equivalent of the fixed-point d. | |||||||
| > > | fx>f ( d -- r ) r is the floating-point equivalent of the fixed-point d | |||||||
| Changed: | ||||||||
| < < | f. ( r -- ) Display, with a trailing space, the top number using fixed-point notation: | |||||||
| > > | f. ( r -- ) Display, with a trailing space, the top number using fixed-point notation | |||||||
| fx* fx/ | ||||||||
Revision 142022-11-02 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 63 to 63 | ||||||||
 | ||||||||
| Added: | ||||||||
| > > | FPU's Dark Corners | |||||||
Some Links | ||||||||
Revision 132022-11-02 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 49 to 49 | ||||||||
| FPU brings reliability allowing to use directly any generated code through a high level tool, such as MATLAB or Scilab, with the highest level of performance. | ||||||||
| Added: | ||||||||
| > > | Any integer with absolute value less than 2^24 can be exactly represented in the single-precision format, and any integer with absolute value less than 2^53 can be exactly represented in the double-precision format. | |||||||
Normalized Numbers Range | ||||||||
Revision 122022-11-02 - PeterSchmid
| Line: 1 to 1 | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | |||||||||||||||||||||||||
| Line: 29 to 29 | |||||||||||||||||||||||||
| Added: | |||||||||||||||||||||||||
| > > | Also from STM AN4044 Floating-point calculations require a lot of resources, as for any operation between two numbers. For example, we need to:
On an FPU-less processor, all these operations are done by software through the C compiler library (or Forth Words) and are not visible to the programmer; but the performances are very low. On a processor having an FPU, all of the operations are entirely done by hardware in a single cycle, for most of the instructions. The C (or Forth) compiler does not use its own floating-point library but directly generates FPU native instructions. When implementing a mathematical algorithm on a microprocessor having an FPU, the programmer does not have to choose between performance and development time. The FPU brings reliability allowing to use directly any generated code through a high level tool, such as MATLAB or Scilab, with the highest level of performance.
Normalized Numbers Range
IEEE.754 Single and Double Precision Floating-Point Coding
Some Links
| ||||||||||||||||||||||||
|
| |||||||||||||||||||||||||
| Deleted: | |||||||||||||||||||||||||
| < < | |||||||||||||||||||||||||
| Deleted: | |||||||||||||||||||||||||
| < < | |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| Line: 39 to 74 | |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| Added: | |||||||||||||||||||||||||
| > > | |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| Deleted: | |||||||||||||||||||||||||
| < < |
| ||||||||||||||||||||||||
| |||||||||||||||||||||||||
| Deleted: | |||||||||||||||||||||||||
| < < |
| ||||||||||||||||||||||||
>float in Gforth engine/support.c verwendet strtod() (strtof() for single precision) | |||||||||||||||||||||||||
| Line: 190 to 221 | |||||||||||||||||||||||||
| --
| |||||||||||||||||||||||||
| Added: | |||||||||||||||||||||||||
| > > |
| ||||||||||||||||||||||||
Revision 112022-11-02 - PeterSchmid
| Line: 1 to 1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner"
image="/twiki/pub/Cosmac/ForthSTM32WB/nucleo-header.jpg" | |||||||||||
| Changed: | |||||||||||
| < < | title="Floating Point Unit (FPU)" | ||||||||||
| > > | title="Floating-Point Unit (FPU)" | ||||||||||
| titlestyle="color:#F00000;"
}%
Intro
| |||||||||||
| Changed: | |||||||||||
| < < | Why Floating Point? | ||||||||||
| > > | Why Floating-Point?
STM AN4044
| ||||||||||
| Deleted: | |||||||||||
| < < | Forth systems traditionally make use of cooperative multitasking. It is very simple and clever. But it has its limits. If you write all your software by yourself, each software part can be cooperative. But if you want to benefit from middleware written by somebody else (and most probably not written in Forth), you can be sure that software is not cooperative (in the context of multitasking). Forth wants to rule your system. I would like to have a Forth system that is cooperative. It should extend the system, to make it interactive and easy to use. | ||||||||||
| Deleted: | |||||||||||
| < < | The Forth interpreter (called terminal task in Forth jargon) itself is only a thread and can be used as some sort of CLI for testing purposes or could be the main part of the application. | ||||||||||
|
| |||||||||||
| Changed: | |||||||||||
| < < | Forth MultitaskingAndrew Haley wrote "Forth has been multi-tasking for almost 50 years. It's time to standardize it" and he is right. I will implement his proposed API for Mecrisp-Cube described in A multi-tasking wordset for Standard Forth
I use the term task here because it is well known in the Forth world, although Mecrisp-Cube make use of threads. Mecrisp-Cube tasks are CMSIS-RTOS threads with user variables. The Mecrisp-Cube (CMSIS-RTOS / FreeRTOS) scheduler is pre-emptive and not round robin (cooperative). Mecrisp-Cube is always multi tasked, you can not switch off the scheduler and therefore there is no
Floating Point Unit | ||||||||||
| > > | Floating-Point Unit | ||||||||||
| Line: 137 to 140 | |||||||||||
|
| |||||||||||
| Changed: | |||||||||||
| < < | Floating Point Words | ||||||||||
| > > | Floating-Point Words
Bare FPU Words (Without C Math Library) | ||||||||||
f+ ( r1 r2 -- r3 ) Add r1 to r2 giving the sum r3. | |||||||||||
| Line: 148 to 153 | |||||||||||
| fabs ( r1 -- r2 ) r2 is the absolute value of r1. fnegate ( r1 -- r2 ) r2 is the negation of r1. | |||||||||||
| Added: | |||||||||||
| > > | f0= ( r -- ? ) flag is true if and only if r is equal to zero f0< ( r -- ? ) flag is true if and only if r is less than zero f< ( r1 r2 -- ? ) flag is true if and only if r1 is less than r2 f~ ( r1 r2 r3 -- ? ) If r3 is positive, flag is true if the absolute value of (r1 minus r2) is less than r3 If r3 is zero, flag is true if the implementation-dependent encoding of r1 and r2 are exactly identical (positive and negative zero are unequal if they have distinct encodings). If r3 is negative, flag is true if the absolute value of (r1 minus r2) is less than the absolute value of r3 times the sum of the absolute values of r1 and r2. | ||||||||||
| f>s ( r -- n ) n is the single-cell signed-integer equivalent of the integer portion of r. s>f ( n -- r ) r is the floating-point equivalent of the single-cell value n. f>fx ( r -- d ) d is the fixed-point equivalent of the floating-point r | |||||||||||
| Line: 155 to 169 | |||||||||||
| f. ( r -- ) Display, with a trailing space, the top number using fixed-point notation: | |||||||||||
| Added: | |||||||||||
| > > | fx* fx/ | ||||||||||
| Changed: | |||||||||||
| < < | C Math Library | ||||||||||
| > > | Words Using C Math Library
fsin ( r1 -- r2 ) r2 is the sine of the radian angle r1 | ||||||||||
|
| |||||||||||
Revision 102022-11-01 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
%DASHBOARD{ section="banner" | ||||||||
| Line: 148 to 147 | ||||||||
| fsqrt ( r1 -- r2 ) r2 is the square root of r1. fabs ( r1 -- r2 ) r2 is the absolute value of r1. fnegate ( r1 -- r2 ) r2 is the negation of r1. | ||||||||
| Added: | ||||||||
| > > | ||||||||
| f>s ( r -- n ) n is the single-cell signed-integer equivalent of the integer portion of r. s>f ( n -- r ) r is the floating-point equivalent of the single-cell value n. | ||||||||
| Added: | ||||||||
| > > | f>fx ( r -- d ) d is the fixed-point equivalent of the floating-point r fx>f ( d -- r ) r is the floating-point equivalent of the fixed-point d. | |||||||
| f. ( r -- ) Display, with a trailing space, the top number using fixed-point notation:
| ||||||||
| Added: | ||||||||
| > > |
C Math Library | |||||||
|
| ||||||||
Revision 92022-11-01 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| ||||||||
| Added: | ||||||||
| > > |
Floating Point Unit (FPU)
Intro
Why Floating Point?Forth systems traditionally make use of cooperative multitasking. It is very simple and clever. But it has its limits. If you write all your software by yourself, each software part can be cooperative. But if you want to benefit from middleware written by somebody else (and most probably not written in Forth), you can be sure that software is not cooperative (in the context of multitasking). Forth wants to rule your system. I would like to have a Forth system that is cooperative. It should extend the system, to make it interactive and easy to use. The Forth interpreter (called terminal task in Forth jargon) itself is only a thread and can be used as some sort of CLI for testing purposes or could be the main part of the application. Forth MultitaskingAndrew Haley wrote "Forth has been multi-tasking for almost 50 years. It's time to standardize it" and he is right. I will implement his proposed API for Mecrisp-Cube described in A multi-tasking wordset for Standard Forth
I use the term task here because it is well known in the Forth world, although Mecrisp-Cube make use of threads. Mecrisp-Cube tasks are CMSIS-RTOS threads with user variables. The Mecrisp-Cube (CMSIS-RTOS / FreeRTOS) scheduler is pre-emptive and not round robin (cooperative). Mecrisp-Cube is always multi tasked, you can not switch off the scheduler and therefore there is no | |||||||
Floating Point Unit | ||||||||
| Added: | ||||||||
| > > | ||||||||
| Line: 108 to 134 | ||||||||
| #endif | ||||||||
| Added: | ||||||||
| > > |
Floating Point Words
f+ ( r1 r2 -- r3 ) Add r1 to r2 giving the sum r3. f- ( r1 r2 -- r3 ) Subtract r2 from r1, giving r3. f* ( r1 r2 -- r3 ) Multiply r1 by r2 giving r3. f/ ( r1 r2 -- r3 ) Divide r1 by r2, giving the quotient r3. fsqrt ( r1 -- r2 ) r2 is the square root of r1. fabs ( r1 -- r2 ) r2 is the absolute value of r1. fnegate ( r1 -- r2 ) r2 is the negation of r1. f>s ( r -- n ) n is the single-cell signed-integer equivalent of the integer portion of r. s>f ( n -- r ) r is the floating-point equivalent of the single-cell value n. f. ( r -- ) Display, with a trailing space, the top number using fixed-point notation:
| |||||||
| Deleted: | ||||||||
| < < | -- | |||||||
| Changed: | ||||||||
| < < | Comments | |||||||
| > > | -- | |||||||
| Deleted: | ||||||||
| < < | ||||||||
| \ No newline at end of file | ||||||||
| Added: | ||||||||
| > > |  This work by Peter Schmid is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. | |||||||
Revision 82022-10-27 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Floating Point Unit | ||||||||
| Line: 8 to 8 | ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
| |||||||
| ||||||||
| Line: 18 to 18 | ||||||||
| ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
| |||||||
>float in Gforth engine/support.c verwendet strtod() (strtof() for single precision) | ||||||||
Revision 72022-10-27 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Floating Point Unit | ||||||||
| Line: 8 to 8 | ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
| |||||||
| ||||||||
| Line: 18 to 18 | ||||||||
| ||||||||
| Added: | ||||||||
| > > |
| |||||||
>float in Gforth engine/support.c verwendet strtod() (strtof() for single precision) | ||||||||
Revision 62022-03-14 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Floating Point Unit | ||||||||
| Line: 7 to 7 | ||||||||
| Added: | ||||||||
| > > |
| |||||||
| ||||||||
Revision 52022-03-14 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Floating Point Unit | ||||||||
| Line: 9 to 9 | ||||||||
|
| ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
| |||||||
| ||||||||
| Line: 18 to 18 | ||||||||
| ||||||||
| Changed: | ||||||||
| < < | >float in Gforth engine/support.c verwendet strtod() | |||||||
| > > | >float in Gforth engine/support.c verwendet strtod() (strtof() for single precision) | |||||||
Cell to_float(Char *c_addr, UCell u, Float *rp)
{ | ||||||||
Revision 42021-08-20 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Floating Point Unit | ||||||||
| Line: 18 to 18 | ||||||||
| ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > | >float in Gforth engine/support.c verwendet strtod()
Cell to_float(Char *c_addr, UCell u, Float *rp)
{
/* convertible string := <significand>[<exponent>]
<significand> := [<sign>]{<digits>[.<digits0>] | .<digits> }
<exponent> := <marker><digits0>
<marker> := {<e-form> | <sign-form>}
<e-form> := <e-char>[<sign-form>]
<sign-form> := { + | - }
<e-char> := { D | d | E | e }
*/
Char *s = c_addr;
Char c;
Char *send = c_addr+u;
UCell ndigits = 0;
UCell ndots = 0;
UCell edigits = 0;
char cnum[u+3]; /* append at most "e0\0" */
char *t=cnum;
char *endconv;
Float r;
if (s >= send) /* treat empty string as 0e */
goto return0;
switch ((c=*s)) {
case ' ':
/* "A string of blanks should be treated as a special case
representing zero."*/
for (s++; s<send; )
if (*s++ != ' ')
goto error;
goto return0;
case '-':
case '+': *t++ = c; s++; goto aftersign;
}
aftersign:
if (s >= send)
goto exponent;
switch (c=*s) {
case '0' ... '9': *t++ = c; ndigits++; s++; goto aftersign;
case '.': *t++ = c; ndots++; s++; goto aftersign;
default: goto exponent;
}
exponent:
if (ndigits < 1 || ndots > 1)
goto error;
*t++ = 'E';
if (s >= send)
goto done;
switch (c=*s) {
case 'D':
case 'd':
case 'E':
case 'e': s++; break;
}
if (s >= send)
goto done;
switch (c=*s) {
case '+':
case '-': *t++ = c; s++; break;
}
edigits0:
if (s >= send)
goto done;
switch (c=*s) {
case '0' ... '9': *t++ = c; s++; edigits++; goto edigits0;
default: goto error;
}
done:
if (edigits == 0)
*t++ = '0';
*t++ = '\0';
assert(t-cnum <= u+3);
r = strtod(cnum, &endconv);
assert(*endconv == '\0');
*rp = r;
return -1;
return0:
*rp = 0.0;
return -1;
error:
*rp = 0.0;
return 0;
}
#endif
| |||||||
Revision 32021-08-17 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Floating Point Unit
| ||||||||
| Added: | ||||||||
| > > |
| |||||||
Revision 22021-07-28 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Floating Point Unit
| ||||||||
| Added: | ||||||||
| > > | ||||||||
Revision 12020-10-27 - PeterSchmid
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Added: | ||||||||
| > > |
Floating Point Unit
Comments
| |||||||
Ideas, requests, problems regarding TWiki? Send feedback